Fibonaccivene | Feynmanin vesinorokaava

Richard Feynman (1918-1988) oli ikoninen leikkisän fyysikon arkkityyppi. Hän on tullut tunnetuksi muun muassa fysiikan luentosarjastaan, kvanttielektrodynamiikan keksimisestä sekä osallistumisestaan atomipommin luoneeseen Manhattan-projektiin. Parhaiten hänen toimintaansa mielestäni kuvaa sananlasku "parhaat ideat saa helpoiten siten, että on paljon ideoita".

Minulle Feynman tuli tutuksi luettuani opiskeluaikoinani teoksen Laskette varmaankin leikkiä, Mr. Feynman! [-1]. Siinä hän viihdyttävästi kertoilee anekdoottejaan, joista monet on hauskoja ja mieleenpainuvia, vaikkakaan osa ei ole kestänyt aikaa. Eräässä tarinassaan hän kertoo siitä, kuinka fysiikkaa ei tarvitse pelkästään käyttää suurien, maailmaamullistavien asioiden keksimiseen, vaan fysiikalla voi myös vain huvikseen leikkiä. Ohimennen hän viittaa tapaukseen, jossa hän lukiolaisena tylsyyksissään kehitti simppelin kaavan vesihanasta virtaavan veden malliksi, muttei avaa asiaa tämän enempää.

Juuri tätä lukiessa, fysiikan opinnoissani analysoitiin Navier-Stokesin yhtälöitä, jotka kuvaavat viskoisten fluidien, eli nesteiden ja kaasujen, liikettä. Ihmettelin, että vaikka Feynman on etevä ja kykenevä fyysikko, niin eihänhän sentään ole voinut lukiofysiikan pohjalta Navier-Stokeseja pyöritellä!

Kuinka siis lukiotason tiedoilla saisi mallinnettua veden virtausta? Tämä oli se ratkaiseva oivallus, joka johti minut Feynmanin jäljille. Uskon, että hän kehitti mallinsa seuraavanlaisista lähtökohdista.

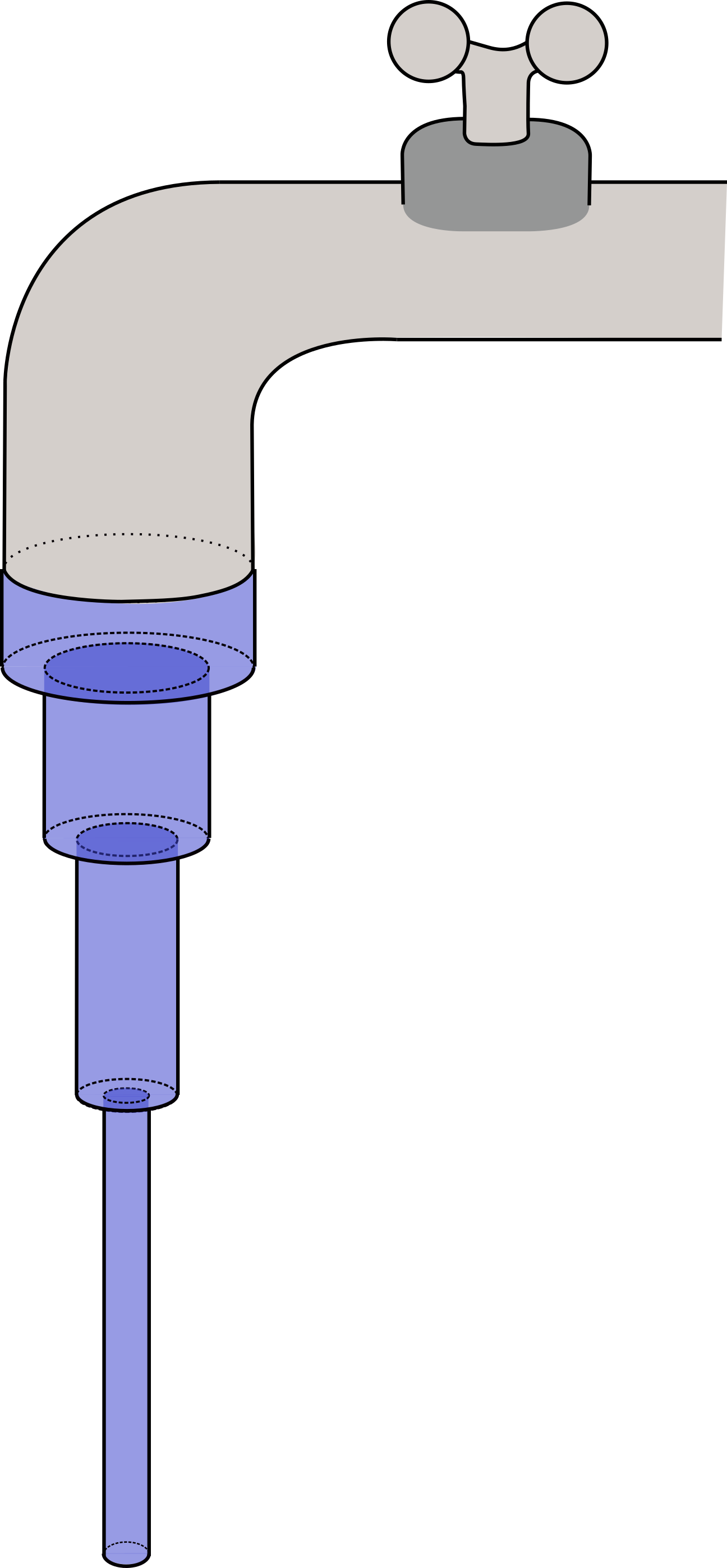
Vesihanasta tippuu vettä vapaasti lähtönopeudella

v_{0}

koko ympyränmuotoisen (säde

r_{0}

) aukon leveydeltä. Täten ajassa

Δt

hanasta valuu sylinterimäinen pätkä, jonka pohja on aukon muotoinen ja jonka korkeus on

v_{0} Δt

. Tilannetta esittävä kaavakuva on alla.

Tämän vesisylinterin nopeus kasvaa gravitaation vaikutuksesta vakiokiihtyvyydellä $g$ ja se on ajan hetkellä $v(t) = gt + v_{0}$ , kuten galileilisesti on tapana. Mutta minkä tähden sitten sylinteri kapenee?

Esikoulun fluididynamiikan oppitunnilla opittiin Bernoullin periaate, jonka mukaan putkessa virtaavan kokoonpuristumattoman nesteen nopeus kiihtyy, jos putki kapenee, sekä vastaavasti virtausnopeus hidastuu jos putki levenee. Matemaattisesti ilmaistuna tämä periaate saa muodon $A_{1} v_{1} = A_{2} v_{2}$ , missä $A_{1}$ ja $v_{1}$ ovat virtauksen poikkipinta-ala ja nopeus yhdessä kohtaa putkea sekä $A_{2}$ ja $v_{2}$ vastaavat suureet jossain toisessa kohtaa putkea. Vaikka vesi tässä tapauksessa putoaa vapaasti, niin veden pintajännityksen takia sylinteri muodostaa ikään kuin putken.

Pintajännitys ei tosin pidä vesinoroa putkena loputtomasti. Kun veden nopeus kasvaa riittävästi, pirstoutuu noro pisaroiksi, eikä nyt johdettava kaava enää päde. Tällöin laminaarinen virtaus muuttuu turbulenttiseksi, joiden analyysi on huomattavasti haastavampaa. Jopa tarkkaa rajanvetoa laminaaristen ja turbulenttisten tilanteiden välillä voi olla myös vaikea tehdä, mutta on olemassa Reynoldsin luku joka antaa osviittaa.

Kaavakuva aukinaisesta vesihanasta. Hanasta valuva vesi on esitetty sylintereinä, jotka kapenevat sitä mukaa, mitä kauemmaksi ne ovat hanasta pudonneet.

Laittamalla algebralootaan nämä kaavat, sekä ympyrän pinta-alan kaavan

A = π r^{2}

, ja ravistellaan, niin saamme vesinoron säteelle $r$ ajanhetkellä $t$ kaavan

[-1] Richard Feynman: "Laskette varmaankin leikkiä, Mr. Feynman!", Kummallisen tyypin seikkailuja, Tähtitieteellinen yhdistys Ursa, 1997.